Kako se kalio čelik
Nešto mi je ovijeh dana dosadno bilo, a dokon um đavolje dvorište. Te se dovatim jedne knjige o AI algoritmima. U pa tu ima svakakve 'euristike, ovi iz Operacionih bi zinuli. Ovde ću kako budem stizao da postavljam neke algoritme. Knjiga ima neke C kodove, sad malo ko parla C, a i ti kodovi su tako odvratni i u knjizi dati iz delova i nepotpuno. Pa sam ih ja sredio u mom omiljenom prog. jeziku.
Prvi algoritam je Simulirano kaljenje. Ima nešto o tome u knjizi iz Operacionih, ali to su pisali matematičari (čitaj: dosadni tipovi). Ideja je da se podražava proces kaljenja. To smo valjda učili iz Teknologije, eto neke koristi i od toga Pa kako se kali? Podigne se temperatura pa se čuka metalni predmet i izvaja u neki oblik, pa se polako 'ladi a i dalje čuka.
U ovom algoritmu se prvo nađe neko najobičnije rešenje, zatim se to rešenje tvikuje (malo se promeni) i gleda kakvo je u odnosu na prethodno. Ako je bolje super, usvajamo ga, ako nije onda po nekoj verovatnoći usvaja. Jer lošije rešenje može u nekoj sledećoj iteraciji voditi u bolje. Usvajanjem ponekog lošijeg rešenja se izbegava nalaženje nekog lokalnog minimuma koji je daleko od globalnog.
E sad da se ne bi mlogo lutalo ta verovatnoća da se usvoji lošije rešenje se iz ciklusa u ciklus smanjuje. To podražava smanjenje se temperatura metala pri kaljenju, što je metal ladniji teže ga je oblikovati. A verovatnoća usvajanja lošijeg rešenja zavisi i od toga koliko je to rešenje lošije. Ako je mlogo loše onda je mala verovatnoća da ga usvojimo.
Znam da vam ništa nije jasno Evo primer primene algoritma. Setite se problema trgovačkog putnika. Postoje algoritmi ali su oni NP-kompletni (u prevodu, teški u p.m za više od 30 čvorova). E sad Simuliranim kaljenjem se dobija rešenje blisko optimalnom ako ne i optimalno (ako vas baš ukenja).
I kako to radi? Pa uzme se neka putanja. Može nasumična može sistemom najbližih čvorova (ovo je bolje početno rešenje). Pa se onda u tom rešenju zamene mesta nekih čvorova i izračuna nova dužina i poredi sa prethodnom. Ako je bolja usvaja se rešenje, ako nije ide po onoj verovatnoći. I tako se iz ciklusa u ciklus smanjuje temperatura sve dok ne padne na neku zaustavnu a pamti se najbolje rešenje. Prosto ko pasulj!
Nemojte da vas uplaši kod, to je prost jezik, a najveći deo koda odlazi na štampanje, što vam nije potrebno da razumete jer je to pythonizovan matlab. Prvo pravimo klasu Grad koja će predstavljati jedan čvor u grafu (__init__ metoda je konstruktor u Pythonu) i definišemo funkciju koja za dati grad iz liste gradova nalazi najbliži:
Potom prvimo klasu za rešenje koje se sastoji od redosleda gradova koje treba obići. Ima metodu za dužinu rešenja (vrednost funkcije cija što bi rekli ćelavi matematičari), metodu za tvikovanja i jednu pomoćnu za grafike. Objekat u konstruktoru automatski nalazi početno rešenje obilaska po metodu idem od čvora do prvog najbližeg dok ne prođem kroz sve:
Ovoj se klasi dodaje i metoda za prikaz rešenja u grafičkom obliku preko matplot biblioteke (i sve to besplatno i slobodno):
I na kraju puštamo u pogon ovu skalameriju koja uz to i radi :)
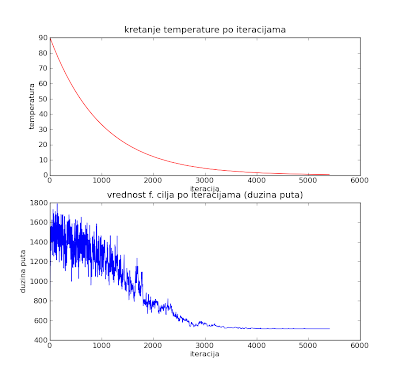
I jedan od rezultata može se prikazati graficima (rezultat metode stampaj_resenje):

Prvi algoritam je Simulirano kaljenje. Ima nešto o tome u knjizi iz Operacionih, ali to su pisali matematičari (čitaj: dosadni tipovi). Ideja je da se podražava proces kaljenja. To smo valjda učili iz Teknologije, eto neke koristi i od toga Pa kako se kali? Podigne se temperatura pa se čuka metalni predmet i izvaja u neki oblik, pa se polako 'ladi a i dalje čuka.
U ovom algoritmu se prvo nađe neko najobičnije rešenje, zatim se to rešenje tvikuje (malo se promeni) i gleda kakvo je u odnosu na prethodno. Ako je bolje super, usvajamo ga, ako nije onda po nekoj verovatnoći usvaja. Jer lošije rešenje može u nekoj sledećoj iteraciji voditi u bolje. Usvajanjem ponekog lošijeg rešenja se izbegava nalaženje nekog lokalnog minimuma koji je daleko od globalnog.
E sad da se ne bi mlogo lutalo ta verovatnoća da se usvoji lošije rešenje se iz ciklusa u ciklus smanjuje. To podražava smanjenje se temperatura metala pri kaljenju, što je metal ladniji teže ga je oblikovati. A verovatnoća usvajanja lošijeg rešenja zavisi i od toga koliko je to rešenje lošije. Ako je mlogo loše onda je mala verovatnoća da ga usvojimo.
Znam da vam ništa nije jasno Evo primer primene algoritma. Setite se problema trgovačkog putnika. Postoje algoritmi ali su oni NP-kompletni (u prevodu, teški u p.m za više od 30 čvorova). E sad Simuliranim kaljenjem se dobija rešenje blisko optimalnom ako ne i optimalno (ako vas baš ukenja).
I kako to radi? Pa uzme se neka putanja. Može nasumična može sistemom najbližih čvorova (ovo je bolje početno rešenje). Pa se onda u tom rešenju zamene mesta nekih čvorova i izračuna nova dužina i poredi sa prethodnom. Ako je bolja usvaja se rešenje, ako nije ide po onoj verovatnoći. I tako se iz ciklusa u ciklus smanjuje temperatura sve dok ne padne na neku zaustavnu a pamti se najbolje rešenje. Prosto ko pasulj!
Nemojte da vas uplaši kod, to je prost jezik, a najveći deo koda odlazi na štampanje, što vam nije potrebno da razumete jer je to pythonizovan matlab. Prvo pravimo klasu Grad koja će predstavljati jedan čvor u grafu (__init__ metoda je konstruktor u Pythonu) i definišemo funkciju koja za dati grad iz liste gradova nalazi najbliži:
class Grad(object):
def __init__(self, x, y, label):
self.x = x
self.y = y
self.label = label
def rastojanje(self, grad):
"""
rastojanje ovog grada od grada primljenog kao prarametar
preko euklidske metrike (odnosno funkcije hypot).
"""
return math.hypot(self.x - grad.x, self.y - grad.y)
def __str__(self):
return "%s(%d, %d)" % (self.label, self.x, self.y)
def _najblizi(pivot, gradovi):
rez = None
min_rastojanje = sys.maxint
for grad in gradovi:
rastojanje = grad.rastojanje(pivot)
if rastojanje < min_rastojanje:
min_rastojanje = rastojanje
rez = grad
return rez
Potom prvimo klasu za rešenje koje se sastoji od redosleda gradova koje treba obići. Ima metodu za dužinu rešenja (vrednost funkcije cija što bi rekli ćelavi matematičari), metodu za tvikovanja i jednu pomoćnu za grafike. Objekat u konstruktoru automatski nalazi početno rešenje obilaska po metodu idem od čvora do prvog najbližeg dok ne prođem kroz sve:
I konačno klasa u kojoj se simulirano kaljenje obavlja. U konstruktoru se prihvata početno rešenje a u metodi start() se dešava ćudo, sa namernim ć :) :
class Resenje(object):
def __init__(self, gradovi=[]):
self.gradovi = [] # gradovi
self.__duzina_puta = None # energija resenja
tek = gradovi.pop(0) # ukloni se prvi od primenljenih
self.gradovi.append(tek) # i stavi kao pocetni
while gradovi:
tek = _najblizi(tek, gradovi) # nadje se najblizi tekucem
gradovi.remove(tek) # on se ukloni iz primeljenih
self.gradovi.append(tek) # i stavi kao sledeci u putanji
def get_duzina_puta(self):
# ako je duzina puta izracunata (prethodno je pozivana grad.duzina_puta)
# i ako u medjuvremenu nije bilo zamene tada je ta duzina i dalje postoji
# i ispravna je. Ovo je jedna optimizacija.
if not self.__duzina_puta:
self.__duzina_puta = self.__racunaj_put()
return self.__duzina_puta
def __racunaj_put(self):
duzina = 0.0
for i in range(len(self.gradovi)):
tek_grad = self.gradovi[i]
sledeci_grad = self.gradovi[(i+1) % len(self.gradovi)]
duzina += tek_grad.rastojanje(sledeci_grad)
return duzina
# duzina_puta je property kao u C#, get metoda je get_duzina_puta
# set metoda ne postoji (read-only property)
duzina_puta = property(get_duzina_puta)
def zameni_put(self):
g1 = random.randrange(len(self.gradovi))
g2 = random.randrange(len(self.gradovi))
while g2 == g1: # obezbedjivanje da g2 != g1
g2 = random.randrange(len(self.gradovi))
# zamena u jednoj liniji bez pomocne promenjive
self.gradovi[g1], self.gradovi[g2] = self.gradovi[g2], self.gradovi[g1]
# prethodno izracunata duzina puta vise ne vazi pa se setuje na None
self.__duzina_puta = None
# pomocna metoda za stampanje resenja
def koordinate(self):
x, y = [], []
for grad in self.gradovi:
x.append(grad.x)
y.append(grad.y)
return x, y
class SimulatorKaljenja(object):
def __init__(self, pocetno_resenje):
self.pocetno_resenje = copy.deepcopy(pocetno_resenje)
self.resenje = None
self.najbolje_resenje = None
self.duzine = []
self.temperature = []
def start(self, pocetna_temperatura=100, alpha=0.999, ponavljanja=10):
tekuce_resenje = copy.deepcopy(self.pocetno_resenje)
privremeno_resenje = copy.deepcopy(self.pocetno_resenje)
najbolje_resenje = copy.deepcopy(self.pocetno_resenje)
tek_temperatura = pocetna_temperatura
ZAUSTAVNA_TEMPERATURA = 0.4
while tek_temperatura > ZAUSTAVNA_TEMPERATURA:
# pamtimo kretanje duzine i temperature kroz iteracije
# da bismo ih kasnije prikazali na grafikonu
self.duzine.append(tekuce_resenje.duzina_puta)
self.temperature.append(tek_temperatura)
for i in xrange(ponavljanja):
privremeno_resenje.zameni_put()
delta_e = privremeno_resenje.duzina_puta - tekuce_resenje.duzina_puta
# ako je privremeno_resenje bolje (delta_e < 0) uzimamo ga
# a ako nije tada uz odredjenu verovatnocu po formuli:
# e^(-delta_e / tek_temperatura) odabiramo losije resenje kao tekuce
# ta verovatnoca je obrnuto srazmerna tek_temperaturi i sto je to novo
# resenje losije (sto je delta_e vece) ono se teze usvaja
if delta_e > 0: print delta_e, tek_temperatura, math.exp(-delta_e / tek_temperatura)
if delta_e < 0.0 or ( math.exp(-delta_e / tek_temperatura) > random.random() ):
tekuce_resenje = copy.deepcopy(privremeno_resenje)
if tekuce_resenje.duzina_puta < najbolje_resenje.duzina_puta:
najbolje_resenje = copy.deepcopy(tekuce_resenje)
else:
# resetujemo privremeno resenje i probamo dalje
privremeno_resenje = copy.deepcopy(tekuce_resenje)
tek_temperatura *= alpha
self.resenje = tekuce_resenje
self.najbolje_resenje = najbolje_resenje
return tekuce_resenje
Ovoj se klasi dodaje i metoda za prikaz rešenja u grafičkom obliku preko matplot biblioteke (i sve to besplatno i slobodno):
def stampaj_resenje(self):
if self.resenje:
try:
# ako je instalirana matplot biblioteka koristi je za graficki prikaz
import matplotlib.pyplot as plt
x1, y1 = self.pocetno_resenje.koordinate()
x2, y2 = self.resenje.koordinate()
x3, y3 = self.najbolje_resenje.koordinate()
# 1. tacku dodajemo ponovo da bi zatvorili konturu od poslednje ka 1. tacki
x1.append(x1[0])
y1.append(y1[0])
x3.append(x3[0])
y3.append(y3[0])
# prvi grafikon
plt.figure(1)
plt.title('prikaz pocetnog i nadjenog resenja')
plt.plot(x1, y1, 'k--', label='pocetno r.')
plt.plot(x3, y3, 'g', marker='.', markerfacecolor='r', markersize=20, label='najbolje r.')
plt.text(2, 95, 'pocetna duzina: %f.2' % self.pocetno_resenje.duzina_puta)
plt.xlabel('x koordinata')
plt.ylabel('y koordinata')
plt.text(2, 87, 'najbolja duzina: %f.2' % self.najbolje_resenje.duzina_puta)
plt.legend()
for grad in self.resenje.gradovi:
plt.text(grad.x, grad.y - 2.5, grad.label)
plt.axis([min(x1) -1, max(x1) + 1, min(y1) -1, max(y1) +1])
# drugi grafikon
plt.figure(2)
# 1. subplot
plt.subplot(2, 1, 1)
plt.title('kretanje temperature po iteracijama')
plt.plot(self.temperature, 'r')
plt.xlabel('iteracija')
plt.ylabel('temperatura')
# 2. subplot
plt.subplot(2, 1, 2)
plt.title('vrednost f. cilja po iteracijama (duzina puta)')
plt.plot(self.duzine)
plt.xlabel('iteracija')
plt.ylabel('duzina puta')
plt.show()
except ImportError:
# nema matplot biblioteke stampaj resenje
print "Pocetno resenje"
print self.pocetno_resenje.gradovi
print "duzina puta je: ", self.pocetno_resenje.duzina_puta
print "\nResenje"
print self.najbolje_resenje.gradovi
print "duzina puta je: ", self.najbolje_resenje.duzina_puta
I na kraju puštamo u pogon ovu skalameriju koja uz to i radi :)
def main():
try:
import psyco # ako je instalirana biblioteka koristi je (ubrzava izvsenje koda)
psyco.full()
except ImportError:
pass
gradovi = [Grad(1, 2, 'a'), Grad(29, 21, 'b'),Grad(100, 60, 'c'), Grad(12, 86, 'd'),
Grad(92, 46, 'e'), Grad(83, 38, 'f'), Grad(55, 36, 'g'), Grad(71, 99, 'h'),
Grad(12, 41, 'i'), Grad(34, 48, 'j'), Grad(69, 33, 'k'), Grad(78, 10, 'l'),
Grad(86, 68, 'm'), Grad(79, 27, 'n'), Grad(22, 69, 'o'), Grad(75, 55, 'p'),
Grad(51, 68, 'r'), Grad(91, 23, 's'), Grad(22, 42, 't'), Grad(47, 80, 'u'),
Grad(60, 10, 'w'), Grad(91, 79, 'v'), Grad(5, 66, 'x'), Grad(42, 90, 'y'),
Grad(23, 59, '1'), Grad(46, 83, '2'), Grad(93, 63, '3'), Grad(47, 17, '4'),
Grad(53, 79, '5'), Grad(76, 23, '6'), Grad(91, 62, '7'), Grad(44, 97, '8'),]
proizvoljno_resenje = Resenje(gradovi)
simulator = SimulatorKaljenja(proizvoljno_resenje)
t0 = time.time()
simulator.start(ponavljanja=10, alpha=0.999, pocetna_temperatura=90)
print "Izvrsenje trajalo", time.time() - t0, "sekundi"
simulator.stampaj_resenje()
if __name__ == "__main__":
main()
I jedan od rezultata može se prikazati graficima (rezultat metode stampaj_resenje):


Comments
($x,$y) = ($y,$x); # Perl
x,y = y,x # Ruby
x ^= y ^= x ^= y; // C i C++
[ x, y ] = [ y, x ] % Matlab