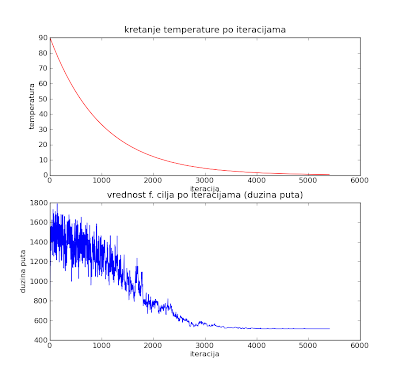
Optimizacija mravlje kolonije
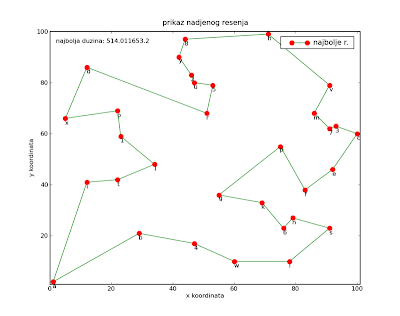
Sad prelazimo sa analogije metalurških procesa na biologiju :) E ta veštačka inteligencija, uvek traže inspiraciju u nečemu postojećem. Ideja je nastala na osnovu proučavanja konunikacije i upravljanja koji se dešava među insektima. Mravi kad traže neki izvor ispuštaju feromone. Feromoni vremenom isparavaju a količina feromona na nekoj stazi zavisi i od dužine staze. Mrav koji nađe kraći put na tom putu će ostaviti veću količinu feromona koji će drugim mravima poslužiti za navođenje na bolju putanju. Pomoću ove ideje moguće je napisati heuristiku za rešavanje problema trgovačkog putnika (nalaženje što kraće Hamiltonove konture). Dovoljno je imati 3 proste formule, toliko proste da su matematičari morali da ih zakomplikuju lupanjem nekih čudnih oznaka, samo im rusko slovo Я fali. To me podseti na epizodu kad sam polagao statistiku kod jedne nemaštovite asistentkinje kojoj je bilo čudno što formulu uslovne verovatnoće nisam izveo identično kao u knjizi, tj. što nisam bubao već pravio de