Zlatno ćoše - Zlatan Kadragić

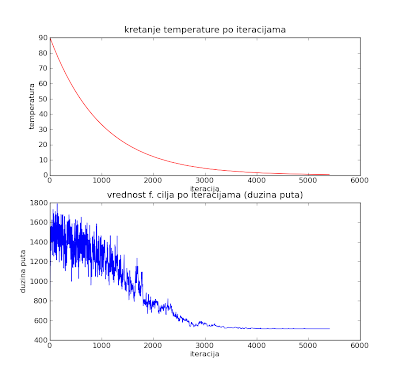
Još jedan problem s kojim se ljudi koji se bave umetnošću programiraju vaćaju u koštac je problem N kraljica. Na tabli N x N treba postaviti N kraljca a da jedna drugu ne jedu. I ovaj problem se može rešiti Simuliranim kaljenjem. Funkcija cilja je u ovom slučaju broj sukoba, samo za razliku od prošlog primera sa trgovcem ovde se zna da je optimalno rešenje kad je f. cilja = 0. Počentno rešenje se lako nalazi. Prvo ne sme se desti da više od jedne kraljce bude u bilo kom redu i bilo kojoj koloni. Dakle najprostije je da se poređaju po dijagonali. U mom rešenju se takvo rešenje tvikuje par puta i dobija se početno rešenje. Tvikovanje se sastoji u nasumičnoj zameni 2 kolone. Implementacija je takva da se u klasi Resenje u nizu koji se zove kraljice čuva pozicija kraljice u redu za svaku kolonu. Npr. niz [1, 0, 2] znači da se u 1. koloni kraljica nalazi u 2. redu, 2. koloni u redu 1, a u 3. koloni u redu 3 (i u Pythonu su prvi elementi niza na poziciji 0). Dakle u početnom rešenju ćemo pre...

Nešto mi je ovijeh dana dosadno bilo, a dokon um đavolje dvorište. Te se dovatim jedne knjige o AI algoritmima. U pa tu ima svakakve 'euristike, ovi iz Operacionih bi zinuli. Ovde ću kako budem stizao da postavljam neke algoritme. Knjiga ima neke C kodove, sad malo ko parla C, a i ti kodovi su tako odvratni i u knjizi dati iz delova i nepotpuno. Pa sam ih ja sredio u mom omiljenom prog. jeziku. Prvi algoritam je Simulirano kaljenje. Ima nešto o tome u knjizi iz Operacionih, ali to su pisali matematičari (čitaj: dosadni tipovi). Ideja je da se podražava proces kaljenja. To smo valjda učili iz Teknologije, eto neke koristi i od toga Pa kako se kali? Podigne se temperatura pa se čuka metalni predmet i izvaja u neki oblik, pa se polako 'ladi a i dalje čuka. U ovom algoritmu se prvo nađe neko najobičnije rešenje, zatim se to rešenje tvikuje (malo se promeni) i gleda kakvo je u odnosu na prethodno. Ako je bolje super, usvajamo ga, ako nije onda po nekoj verovatnoći usvaja. Jer lošij...